Scene 1 (0s)
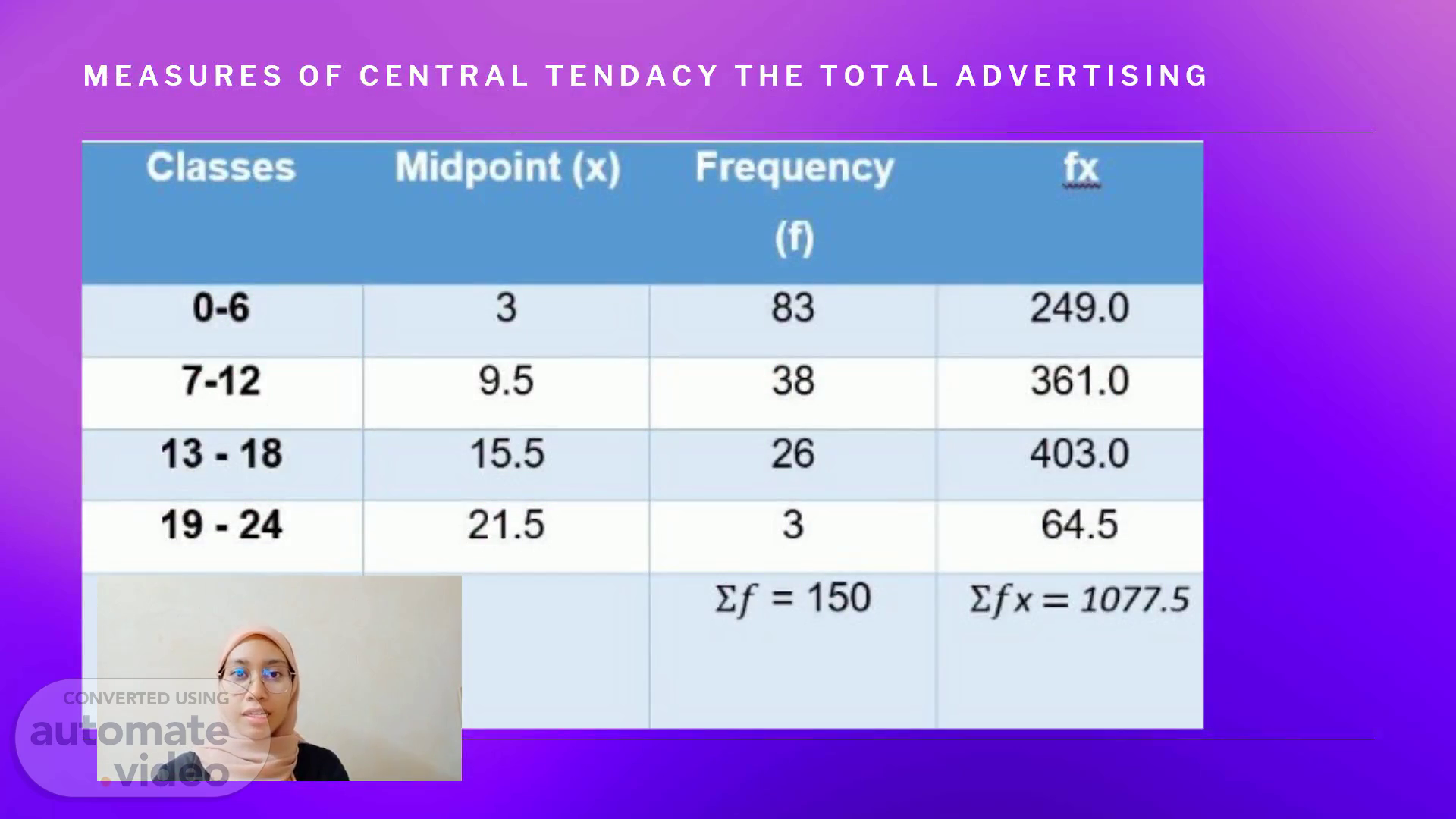
MEASURES OF CENTRAL TENDACY THE TOTAL ADVERTISING.
Scene 2 (24s)
Mean: x = Ʃfx n Where x = midpoint of a class f = frequency of class n = Ʃf (number of entries in sample) Mean: x = Ʃfx n = 1077.5/150 = 7.18 (the mean of the total advertising budget was approximately 7.18).
Scene 3 (44s)
Median = Mm = ∫+ (n/2-cf/f)h = 0+ (150/2-0/83) 6 = 5.42.
Scene 4 (1m 4s)
mode=L_m+[Δ_1/Δ_1+Δ_2 ]×c. = -0.5 + ⌊83/83-45⌋6 = 132.
Scene 5 (1m 25s)
Classes Frequency (f) 31 76 5-8 39 13-16 4 = 150 Midpoint (x) 2 6.5 10.5 14.5 fx 33.0 494.5 409.5 58.0 Efx = 995.
Scene 6 (1m 36s)
Mean: x = Ʃfx n Where x = midpoint of a class f = frequency of class n = Ʃf (number of entries in sample) Mean: x = Ʃfx n = 995/150 = 6.63.
Scene 7 (1m 51s)
Mm = ∫+ (n/2-cf/f)h Where I = lower limit of median class n= number of observations cf = cumulative frequency of class preceding the median class f = frequency of median class h = class size (assuming class size to be equal).
Scene 8 (2m 8s)
mode=L_m+[Δ_1/Δ_1+Δ_2 ]×c. mode=L_m+[Δ_1/Δ_1+Δ_2 ]×c.